無料ダウンロード 三角形��比の定理 証明 299910-三角��と比の定理 逆 証明

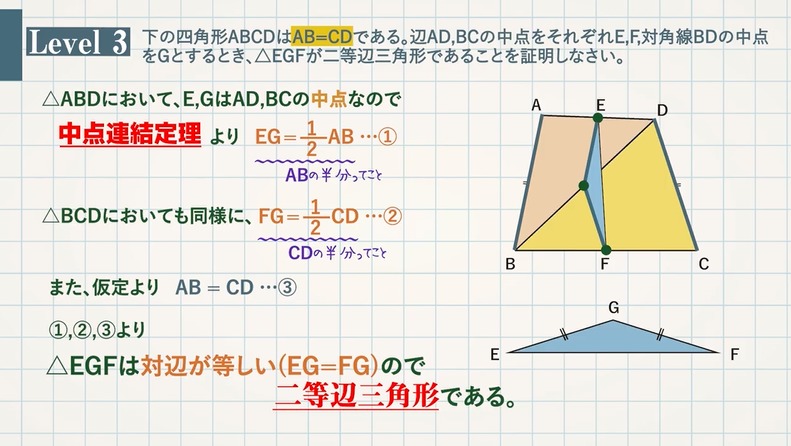
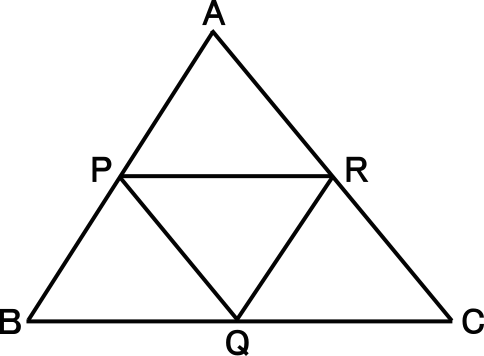
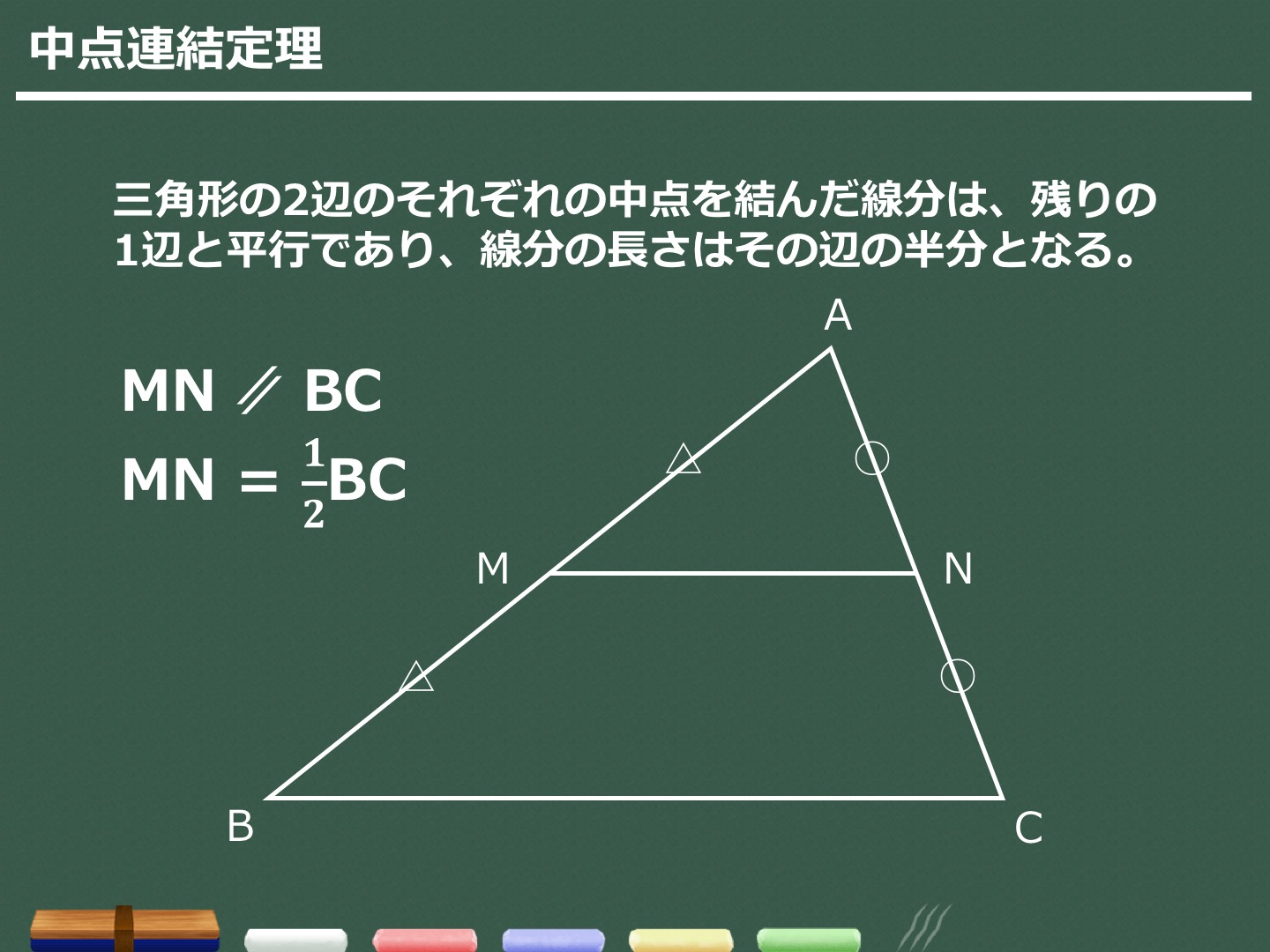
Tossランド 中点連結定理
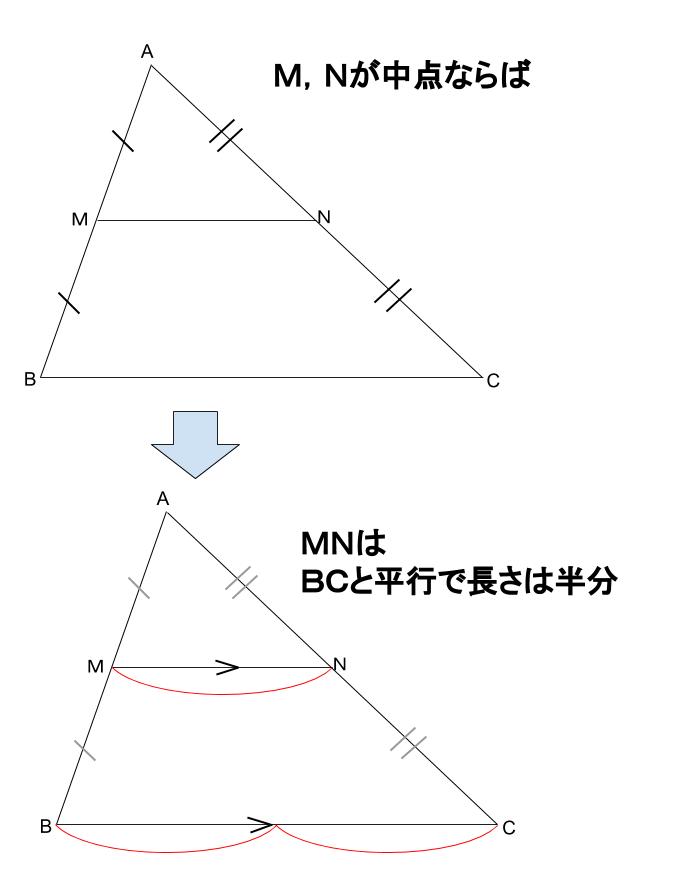
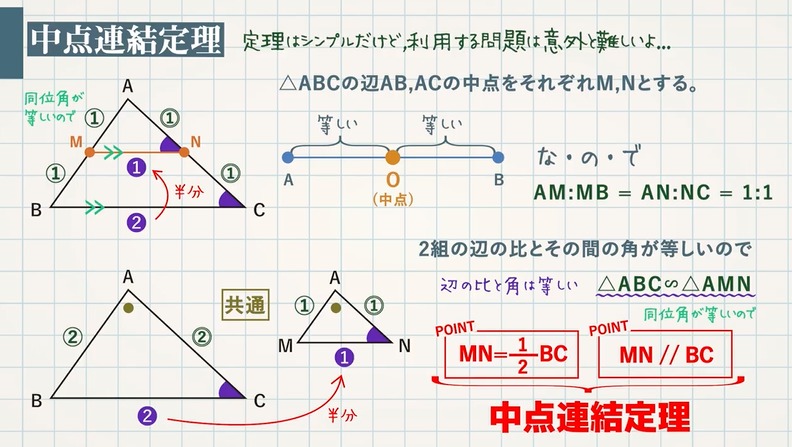
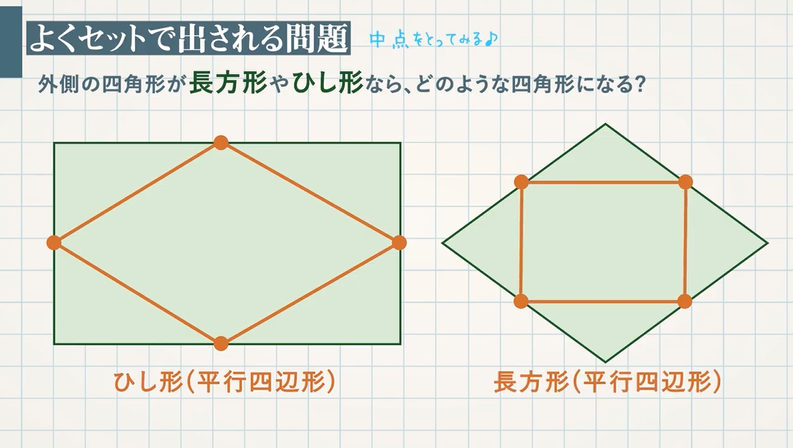
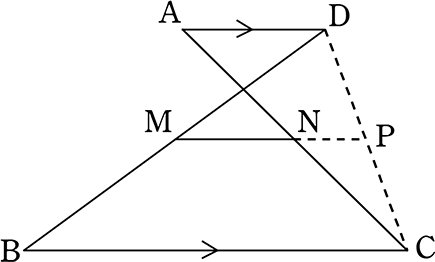
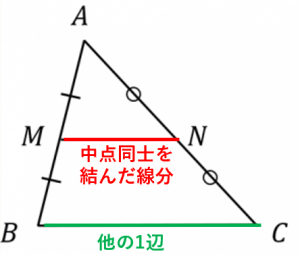
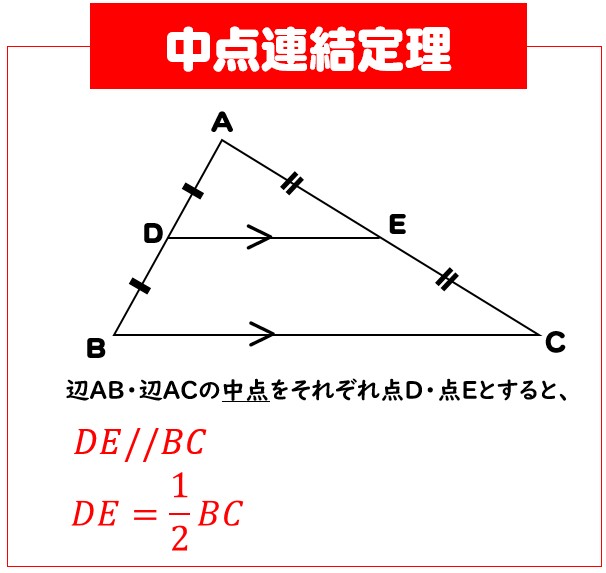
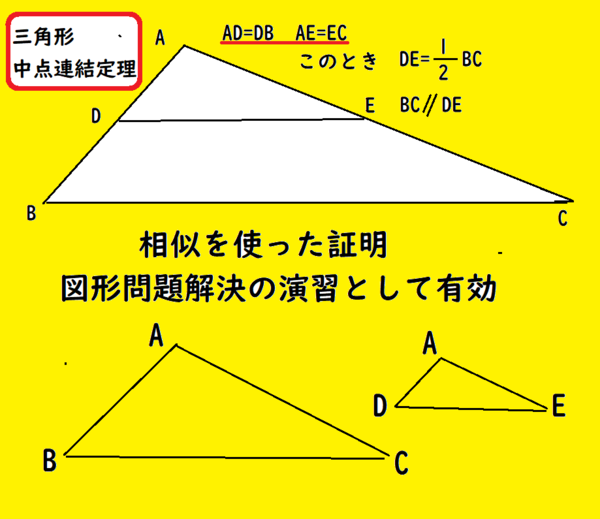
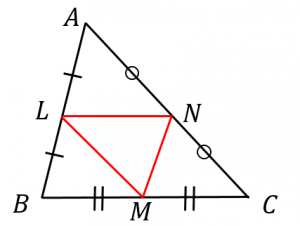
三角形と比の定理の逆を理解し、その定理の逆を利用することができる。 2 三角形と比の定理の逆 1 相似な図形の面積重要なのは、中点連結定理の逆も成り立つという事実です。 つまりBC//MN、かつ M N = 1 2 B C の場合、点Mと点Nは辺の中点です。 以下のように証明できます。 ABCと AMNにおいて ∠BAC=∠MAN:共通の角 – ① ∠ABC=∠AMN:平行線の同位角は等しい – ② ①、②より、2組の角がそれぞれ等しいため、 ABC∽ AMN また M N = 1 2 B C なので、 ABC∽ AMNの相似比は2:1です。
三角形と比の定理 逆 証明
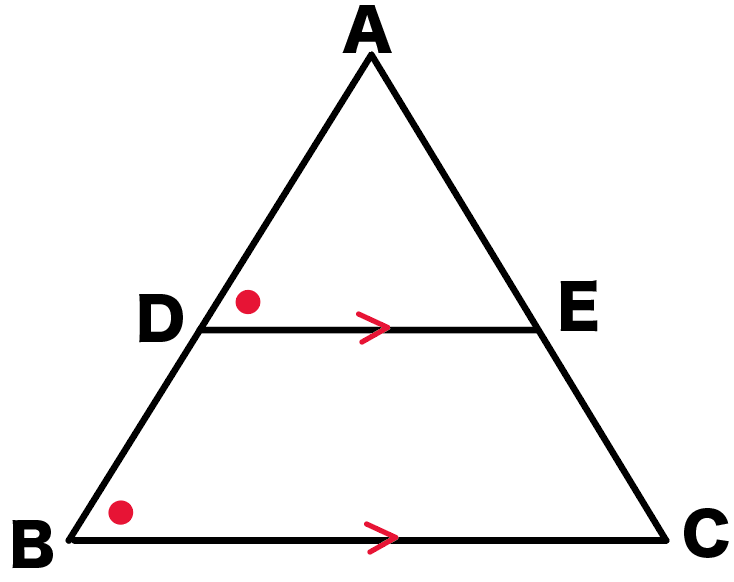
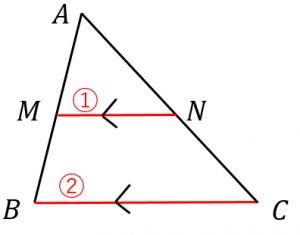
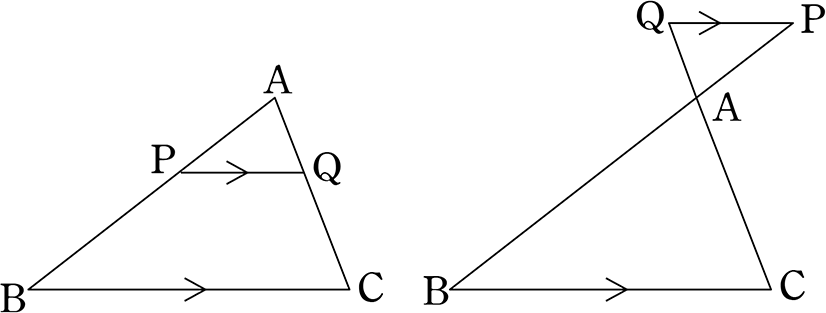
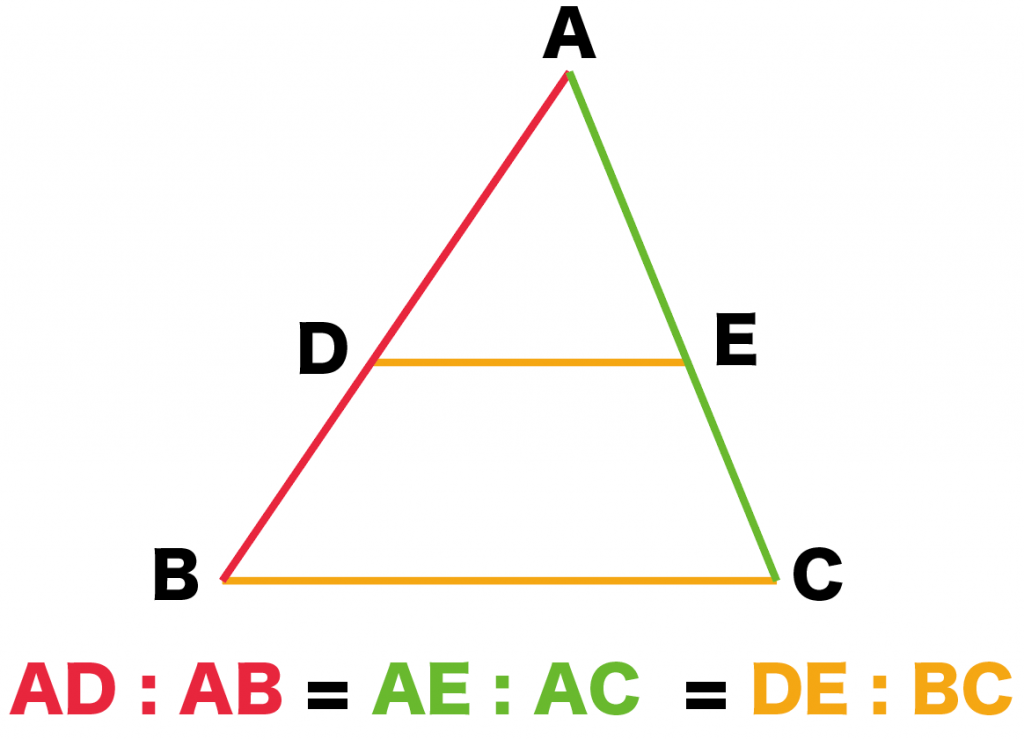
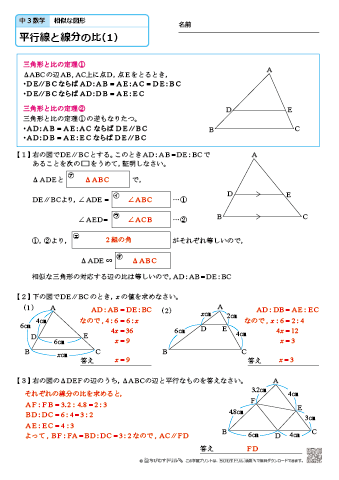
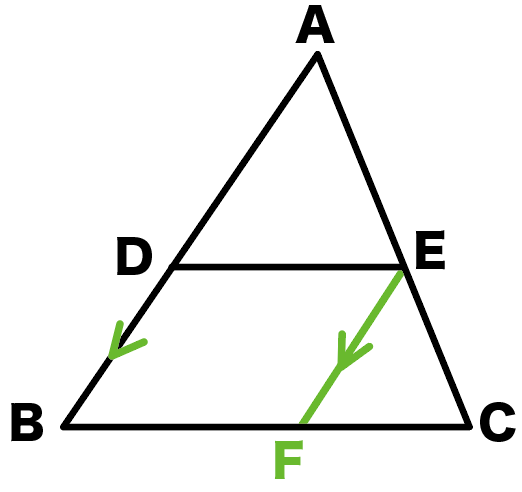
三角形と比の定理 逆 証明- 三角形と比の定理の逆の証明 三角形と比の定理の逆の証明 ABCの辺AB,AC上にそれぞれ点P,Qがあるとき、次のことが成り立つことを証明せよ。 APPB=AQQCならばPQ∥BC 宜しくお願いします。 もし相似を使うなら、相似条件もはしょらずに書いてください。 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。 ルールは 2つの図形のパターン について 覚えておきましょう! 1つ目のパターン 前提として 図のように DEとBCが平行(DE//BC) である必要があります。 (この前提を 忘れないでくださいね! ) すると 次のような

三平方の定理およびその逆 証明 理数系学習サイト Kori
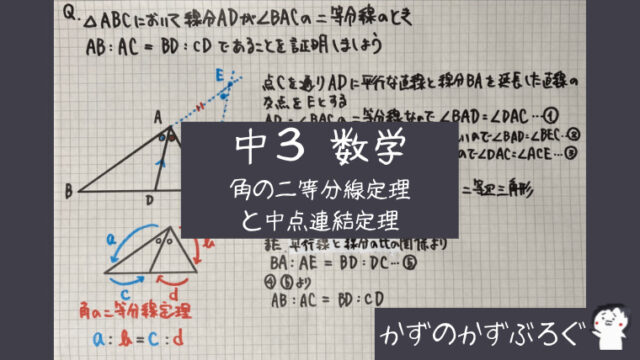
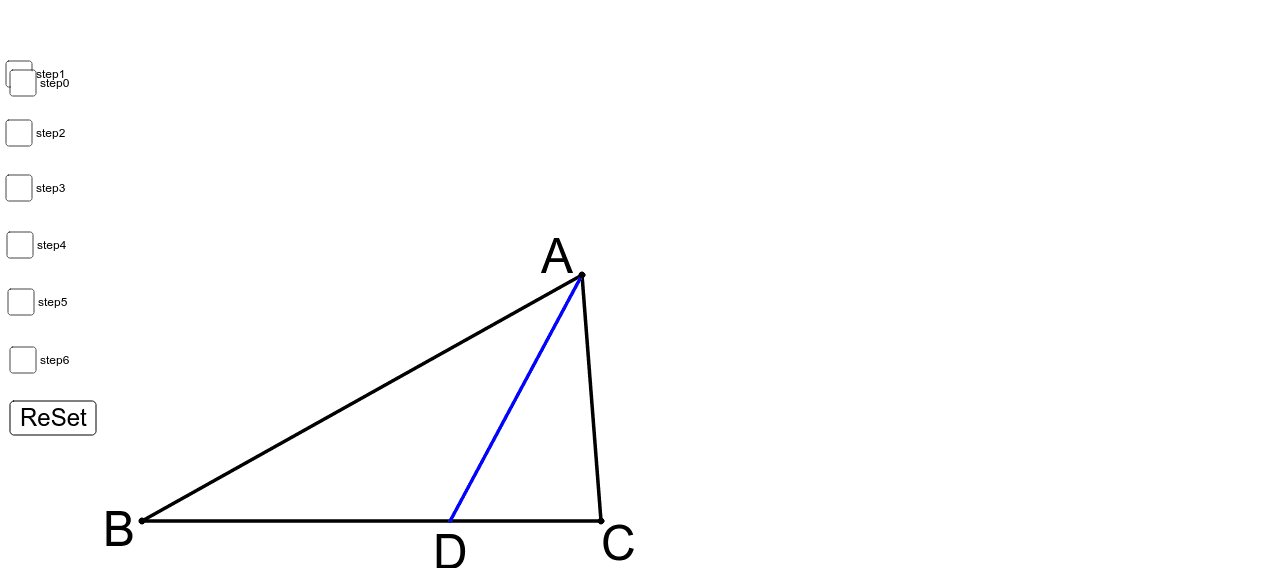
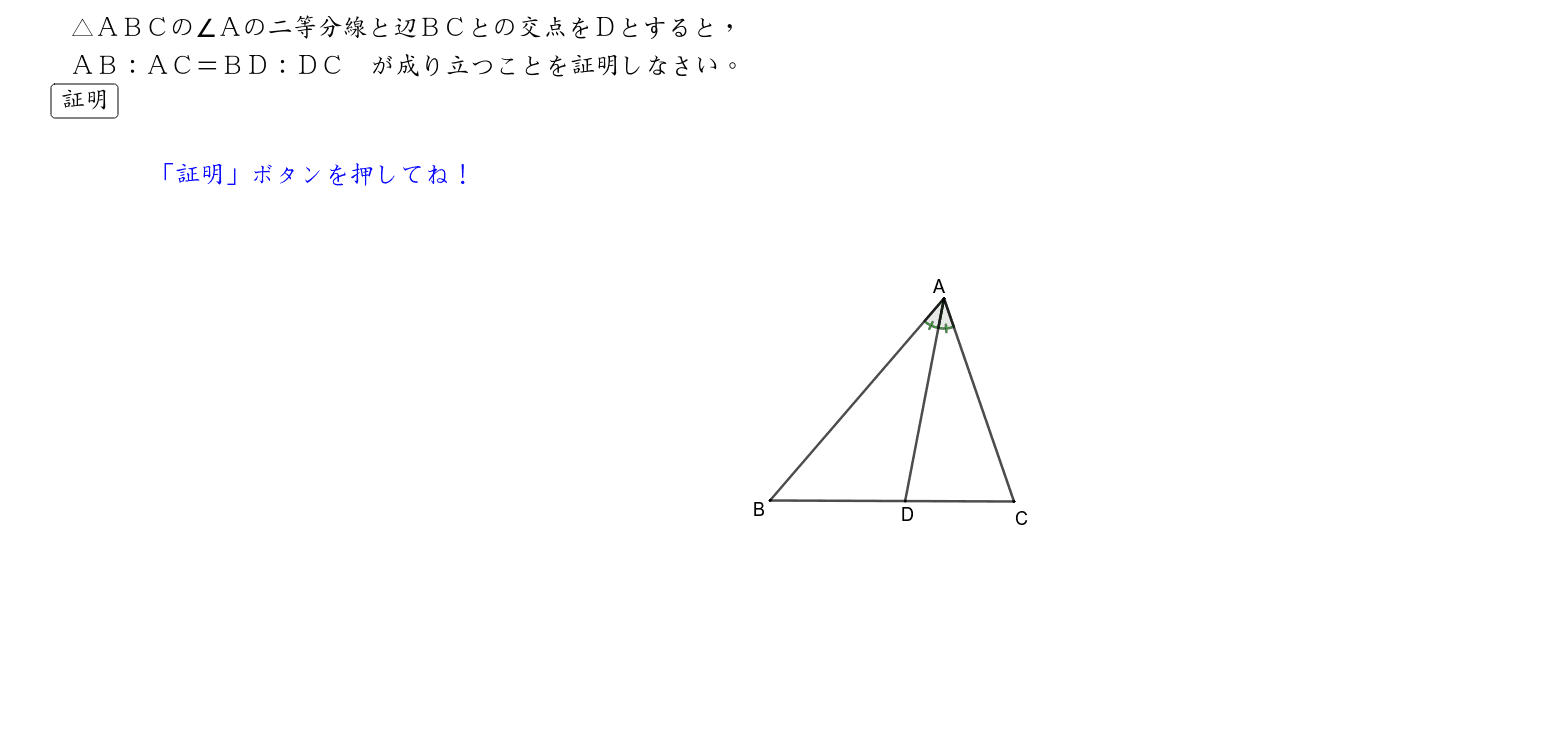
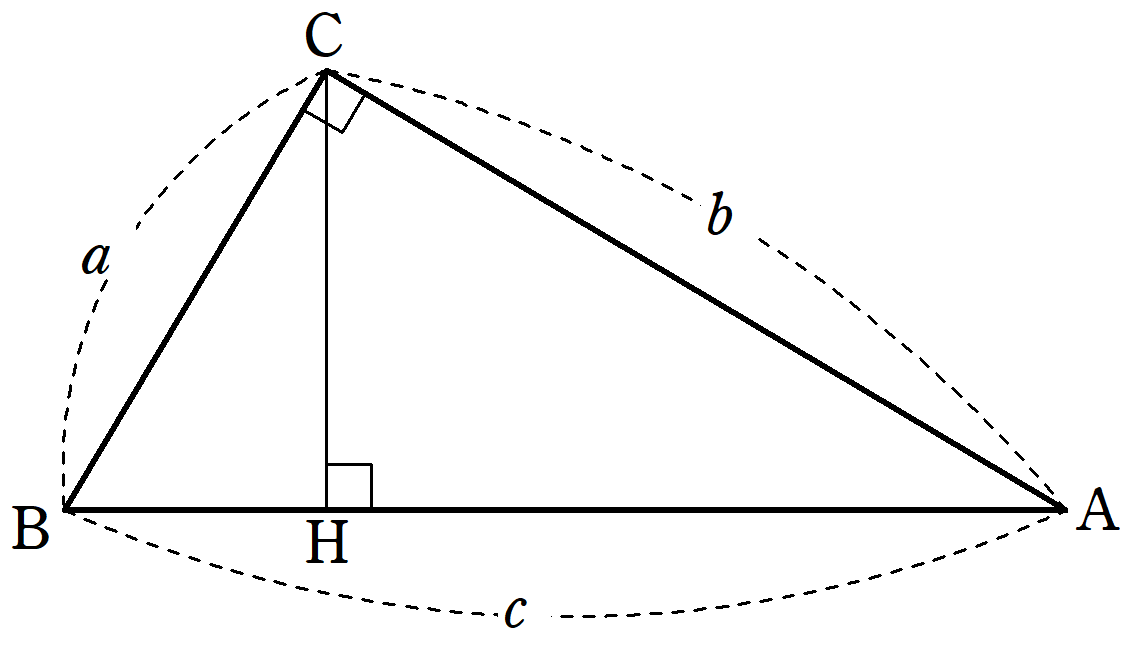
三角形と比の定理の逆の証明 abcの辺ab,ac上にそれぞれ点p,qがあるとき、次のことが成り立つことを証明せよ。 appb=aqqcならばpq∥bc 宜しくお願いします。 もし相似を使うなら、相似条件もはしょらずに書いてください。三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 ここで、斜辺とは、直角三角形の直角に対する対辺のことです。 三平方の定理は、別名、 ピタゴラスの定理 とも呼ばれます。 三平方の定理(ピタゴラスの定理) 3 辺の長さが a, b, c の直角三角形 上の直角三角形において(n 角形の外角の総和) = 360° 2 三角形の内角と外角の関係 a x = 3 凹四角形の角度の関係 a x = 4 角の二等分線に関係する辺の比や長さ b ab ac = be ec = bf cf ae=√ab×ac−be×ec 5 正三角形の辺と高さの比、面積 a h= √3 2 a (面積)= 2 √3 4 a 6 方べきの定理
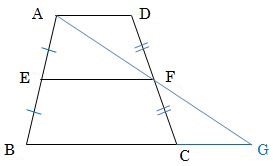
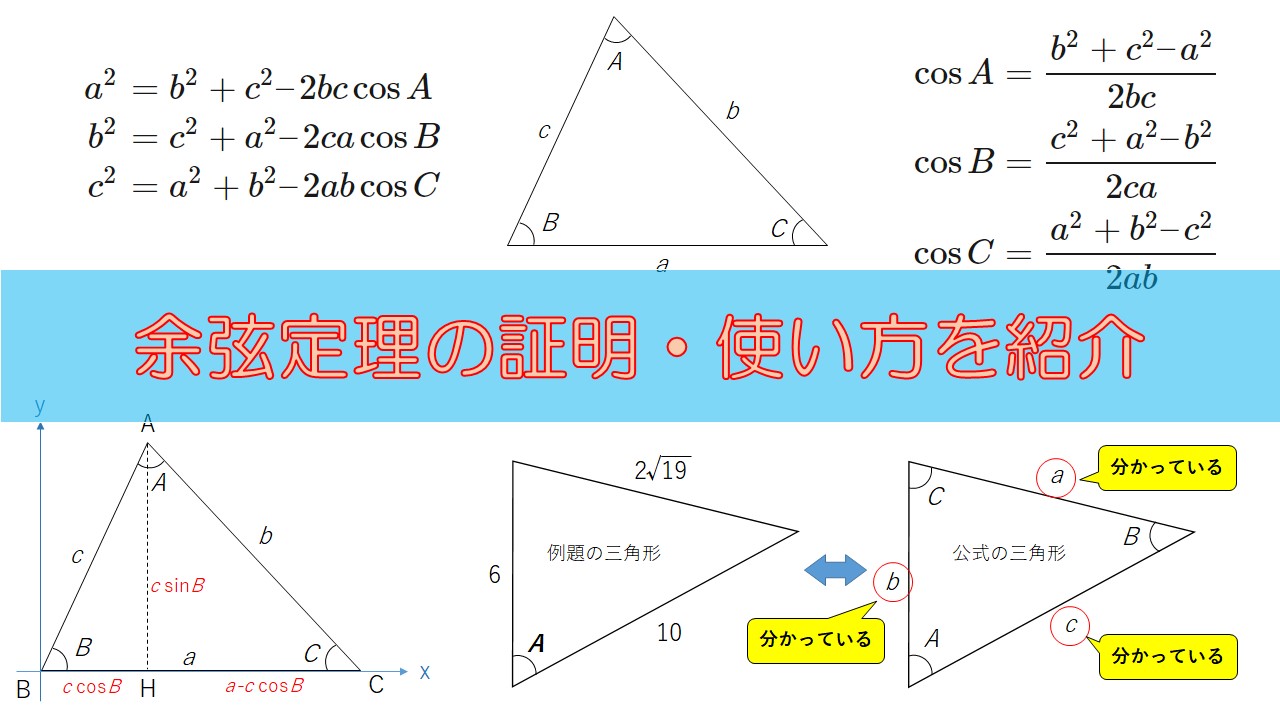
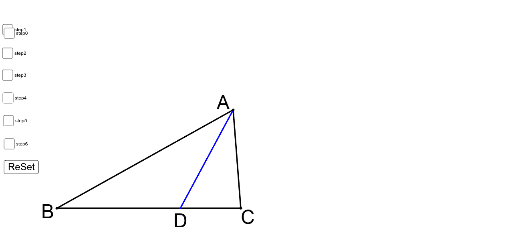
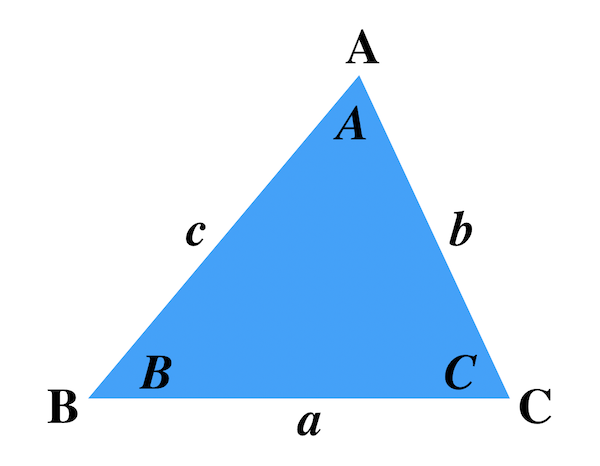
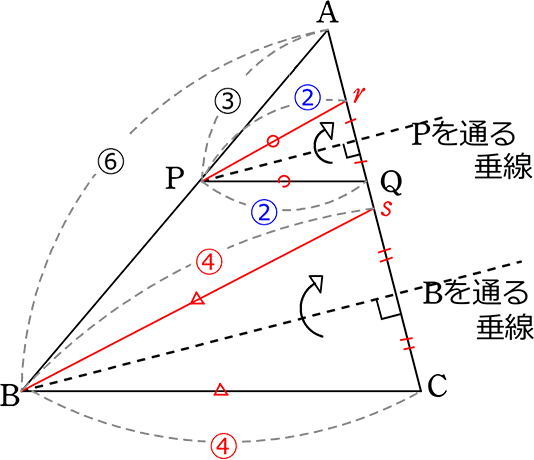
正弦定理は円周角の定理を用いることで証明できます.以下の証明では,鋭角三角形,直角三角形,鈍角三角形の場合にわけて示しています. 証明: ABC A B C において, BC = a,CA = b,AB = c B C = a , C A = b , A B = c ,外接円の中心を O O とします. Case1: C aB a \dfrac{b}{a} a b は x y xy x y 平面において原点と (a, b) (a,b) (a, b) を通る直線の傾きであるという 事実を使うことで加比の理は図形的に理解できます。 証明1.三角形と比の定理の逆を次のように証明した。 空欄をうめなさい。 A <仮定> AD:DB=AE:EC <結論> DE//BC <証明>点Bを通り,辺CA に平行な直線と,ED を延長した 直線との交点をFとする(BF//AE-①)。 (ADE)と (BDF)で 対頂角だから,( ∠ADE=∠BDF)-② F D E 錯覚だから,( ∠DAE=∠DBF)-③ ②,③から (2組の角がそれぞれ等しい)ので (ADE)∽
三角形と比の定理 逆 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
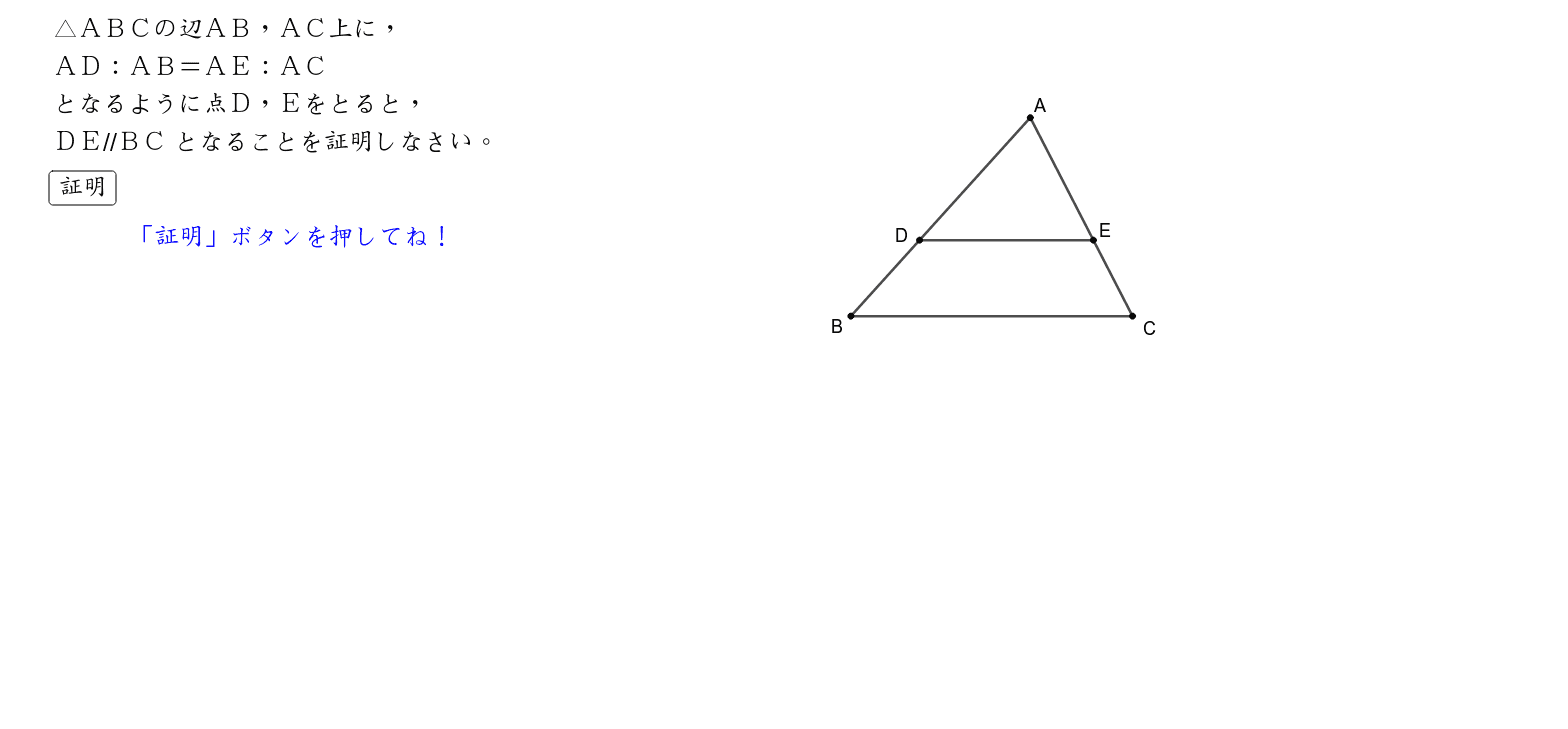 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形と比の定理 逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
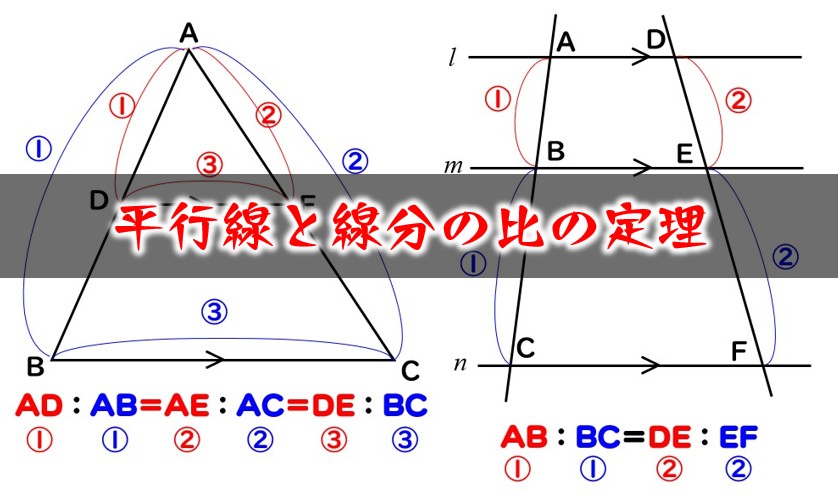 |  |
平行線によって比が移ったと覚えてもいいよ。 これから何故比が同じなのか三角形の相 似を利用して証明をしていこう。 ↓クリック! まとめ! 三角形と比の定理 ABC において、 点D、E をそれぞれ 辺AB、AC 上、また はその延長上の点とするとき次のことがいえる。 ①DE//BCならばAD:AB=AE:AC=DE:BC ②DE//BCならばAD:DB=AE:EC この定理は下図のような場合も三角形と比の定理の証明1 新しい教材 アステロイド 斜めドップラー 接点の作る円は内接円 直方体の対角線 sinewave 教材を発見 三角関数とは? χ二乗検定問題 円と楕円 tetranball 外角と内角の関係
Incoming Term: 三角形と比の定理 証明, 三角形と比の定理 逆 証明,
コメント
コメントを投稿